A Monte Carlo simulation (or probability simulation) is a technique for modeling the probability of different outcomes in processes where random variables make the outcome difficult to predict. Rather than replacing uncertain variables with a single average number, Monte Carlo simulations run many different possible variables. In finance, Monte Carlo simulations are used to estimate the probability of cost overruns in large projects as well as predict asset movement. Analysts also use Monte Carlo simulations to determine the probability of an entity defaulting, and for analyzing derivatives such as options.
Monte Carlo simulations begin with a mathematical model for the desired process being tested. Random variables within an appropriate range are then placed inside the uncertain parts of the model, with the outcomes plotted as a probability distribution curve. Ideally, these types of simulations are run by computers tens of thousands of times in order to test all possible outcomes. Decision makers can then look at the accumulation of plotted curves to see a range of probable outcomes, and make judgments accordingly.
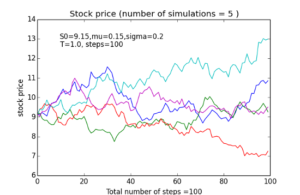
A Monte Carlo simulation for a stock price that has been run five times. Image Credit: Sc1171 (CC by SA-4.0)
Monte Carlo simulations derive their name from the famous casinos of Monte Carlo. Like a slot machine lever that is pulled many times, a Monte Carlo simulation uses randomness to produce a variety of outcomes. The concept was developed by mathematician Stanislaw Ulam, a veteran of the Manhattan Project. While recovering from brain surgery, Ulam reportedly played many games of solitaire, which in turn inspired him to come up with a simulation that could map a wide range of outcomes.

Recent Comments